Introduction to the Sextant

It's not magic, it's just triangles.

Introduction

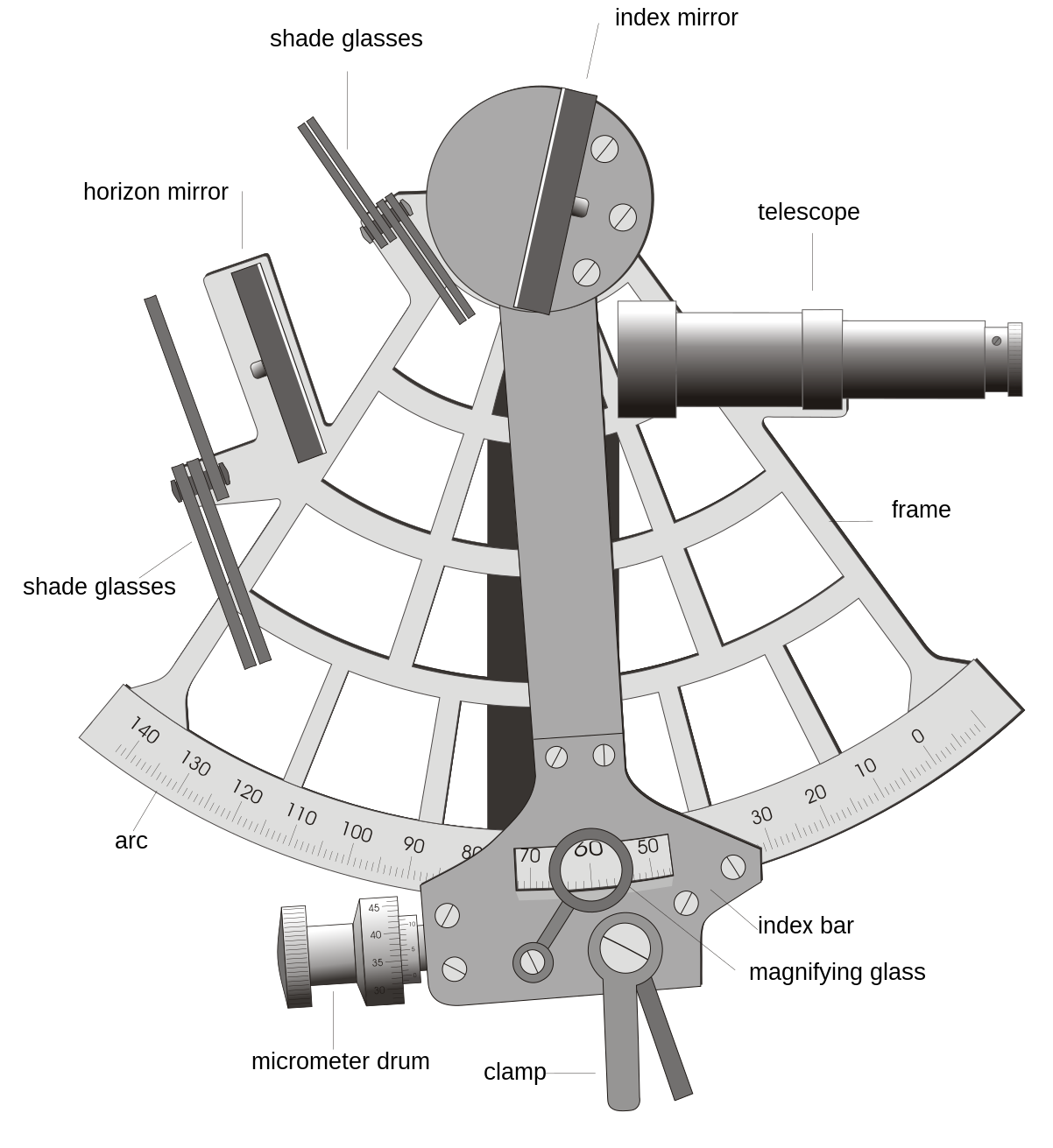
For centuries the sextant was the primary tool for navigation used on ships, and in airplanes. Until the invention of radio and later satellite navigation. But how does a sextant work? Well, to be short it's an angle measurement tool. For measuring angles between the horizon and a celestial object, like the sun, moon, stars and planets.

Horizon

To be able to make such measurements, you need to see both the celestial object and the horizon. The horizon at sea, to be precise, not on land. Because land is irregular, it has hills and shrubbery, and all kinds of other funny land things. The horizon at sea is literally the visual edge of the world. Because we're on a globe and we can't see around the corner. We know for a fact how large the earth is, so we can calculate how far away the horizon is.

To do this the Height of Eye is part of the formula.

Twilight

To be able to see both the object and the horizon, unless it's the sun, we can only do this during Nautical Twilight. The few minutes just before sunrise and just after sunset. Where the stars are visible and the horizon is still clear.

Dead Reckoning

Before we start, we have our approximate position. We know our last position, and from that point we take the ship's course and speed and measure out where we think we are, that is called dead reckoning. If you know your ship, you can guesstemate how much the wind has pushed you off course. And with the information found in the Atlas, you can approximate your drift, how far the current has pushed you. But it's not a precise position.

Astronomy

But with that position as a base point, we know which stars should be visible in which direction and we know, from the book, at which height they should be. Our sciency friends, the astronomers, have all calculated this in advance, the big nerds they are.

Shooting a star

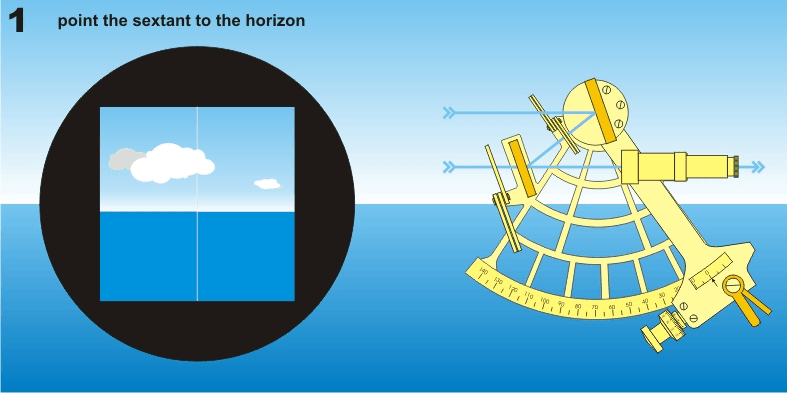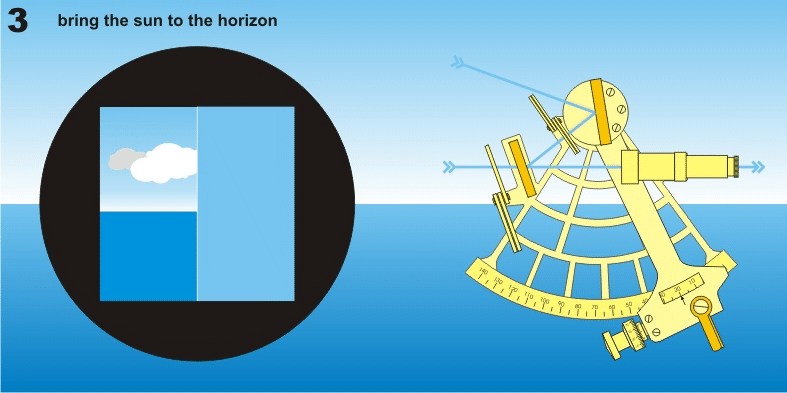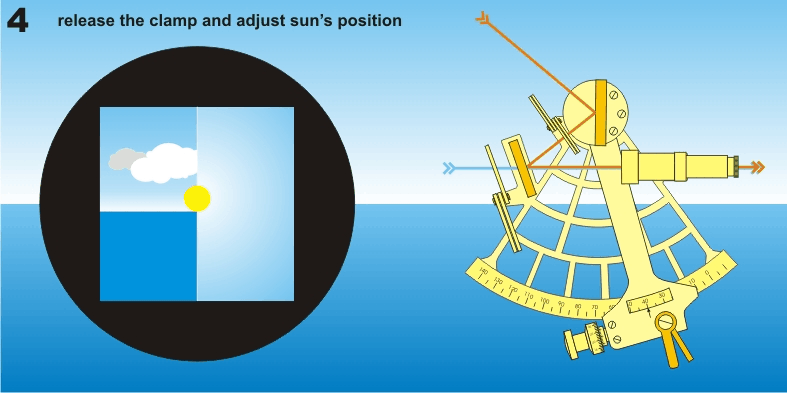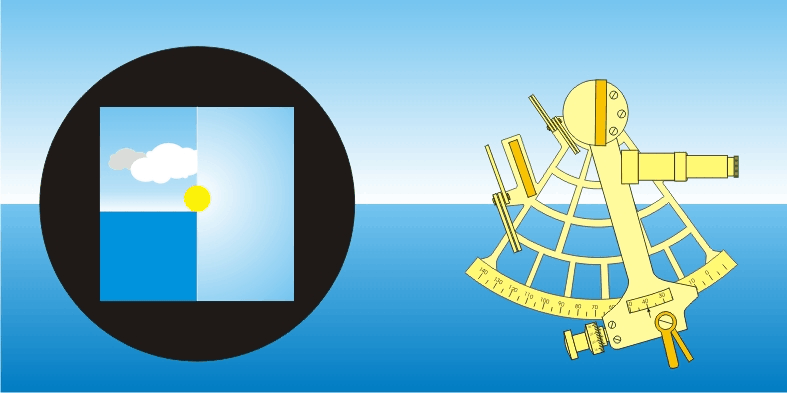
Anyway, we know now we are looking at a star, in the north, at 53 degrees of height, so we can look at the compass and start off facing the right direction. And we can set our sextant at 53 already. Then we look through the sextant keeping the oculus horizontal, and match up the horizon to the centre of your viewing hole. Then we manipulate the lever of the sextant until we can see our star overlaying the horizon. And we measure for instance 52,99°.

We can see both overlaying because we are looking through a mirror that only works half. You are looking up at the star and straight at the horizon at the same time.

As soon as we got the two lined up, we call out, and our friend standby will write down our height measurement, the direction we view the star and the time. That is very important the correct time. Ideally, we do this for six stars. Spread out in six directions, in three opposing pairs. Every time two measurements opposing each other.

Mathematics

And now the fun bit starts!
Mathematics!

With our measurement and the time, we can calculate what the angle should be, according to the astronomeners. And with some trigonometry of the difference between the two angles, we know the distance away we are from spot where the star shines directly down on earth. But this distance is true for a circle all over the globe, everywhere on this circle, we are that distance away from the star. That is why we also measure the direction we view the star in. That would give an intersection between our bearing and our LOP. That's what we call this circle, a LOP, a Line Of Position. This intersection could give us our position, but that is not accurate enough.

Accuracy

But nothing is as accurate as taking a measurement of a star from the deck of a moving ship. Therefore, we've taken also an opposing star. These two circles should line up. If they do not, we have a known fault in our measurement, which we can, and have to, correct for.

The same way we do it for the other four stars. If everything is perfect, all the lines should intersect at exactly the same spot. But it hardly ever is perfect is it?
Usually a little area will appear lined out by all the LOP's with the ship's Most Probable Position, somewhere in there.
This area's somewhere between 0,01 nm² to 1 nm² big. That is more than accurate enough for sailing at the ocean. If it's bigger, you weren't accurate enough in your measurements or made a msitake

By the time you are done with this calculation, you have sailed out of that spot, anyway. But know you know where you were about a quarter of an hour ago. And from that spot, you can continue to estimate your position with your known course and speed.

Now you also know how far the wind and current has pushed you off course in the time between the last two measured postitions, you can correct for that, and take this information into account for your continuous dead reckoning.

Measuring the Sun at Noon

At sunrise, you can do it all again. And then at noon (Ship Time), we can determine at which time, [tooltip:Greenwich Mean Time]GMT, the sun is at its highest point, from the ship's position. You take the sextant again, and point it south, or north if you are in the south. And start looking at the sun. Flip down those shades tho mate, you need your eyes to last a bit longer. Anyway keep following the sun by adjusting the angle. as soon as the sun stops going up, you stop and check the time. If you measure the sun at 22:01 UTC in the top, you know you moved 10 hours and 1 minute to the west of Greenwich. Because at the prime meridian, the sun will be in the highest position at 12:00, noon.

10 hours and 1 minute multiplied by 15 degrees, gives us 150 degrees and 15 minutes West. I hope you are supposed to be in the Gulf of Alaska then, otherwise you messed up your mathematics! But taken into account it's freaking cold I bet we are here.

It's 15 degrees, because the earth is 360 degrees all around and there are 24 time zones, 360 divided by 24 is 15 degrees.

Overcast for days

But what if it's clouded all the time? Well then you just keep going with the dead reckoning till it's not clouded my friend. Or until you reach areas where you think it's too dangerous to keep going. You put a lookout on the bow with a sounding line and start looking for that shallow you may or may not hit if your un-updated guessed position is anything close to where you really are.

But if you see any Navigational Aids, fancy words, for buoy's lighthouses, lightships, church towers, chimneys. Any landmark, or even a natural landmark, that is also on your trusty paper map. You can use those to find your position at any time of the day. Or if they have a Light, also at night!

(How to recognise which light is which, I will explain: Here)

Visual Bearing

You simply look over your compass to measure the angle at which you see the objects. Draw a line on the map, and bam, at the intersection you are.
Maybe.
Did you correct the first line for the speed the ship is going with?
No you didn't did you?
You take that line, move it along your course line in the same way the ship is travelling, the distance you sailed in the time between your two measurements.
See how the intersection of the two visual bearings has shifted.
Yes, that is where you are. Half a mile further along!

Broken Compass

But what if your compass is broken? Well first of all, how the freaking fuck did that happen?!
Go look under the Captain's bed! The spare must be there, in a box probably still sealed from the shipyard.
What do you mean all the alcohol leaked out?
Leaked?
Yeah sure.
Well back to the sextant it is!

Horizontal measurements with a sextant

First flip the thing sideways. Now you do not line up the horizon with a celestial body. No, you line up that buoy and the lighthouse. You measure the angle between them. Idially we do two such measurements between three points. But two can do too.
And with some nice trigonometry, you can know where you are again. Simple as that.

Height measurements

Also you can measure the height of the lighthouse, church tower, chimney stack, or mountain, with your sextant. From the base to the top. That height is on the map too, or if not, then it is in this marvellous book over here no-one ever bothers to look in.

The light house is 65 meters tall, you see, it says here on the map. What did you measure? Three degrees? So how far are we away from it then?
Did you adjust your maths for your height above the water? The height of your eye?
And what is the tide? How high is the water compared to the land? Because you are measuring across two mediums now, water and land. Adjust for all that. And then you can take the divider out and mark how far we are form the light house on the map.

Range finding.

Did you know you can do range finding with a sextant too? Ideally, you need two. Check again under the old man's bed. There is a spare sextant somewhere too.

Now, we just found out we can measure the angle horizontally between two points away from us, to find out where we are. But now we need to find out how far away that one ship is from us.

You go to the bow, all the way to the forward, yes. Now you measure the angle between the mainmast and that other ship.
I'll stay here all the way at the stern, and do the same thing.
The centre line of our ship, the distance from bow to stern, is a thing we know. We take that as the base of our triangle, we just measured the two other angles. And now we can calculate how far away that other ship is.

Secret Mission by Dr. Anvil (Dimitris & Janet)

Sextant by Wikimedia Commons

Sextant by Joaquim Alves Gaspar via wikimedia commons

Using a sextant by Joaquim Alves Gaspar via wikimedia commons

Two crewman are using a sextant. by Willem van de Poll, via wikimedia commons

Etymology

The frame of the sextant is about sixty degrees, or one sixth of a circle. The name comes from the Latin word sextantis, meaning one sixth. (But due to it's mirror set up it can measure over an arc of one hundred and twenty degrees)

Octant

An Octant is the predecessor from the sextant, but it being only one eighth of a circle, the range was to small so the sextant came about.

Related Items

• Pirate ship

Spherical trigonometry with intersecting circles. by Peter Mercator via wikimedia commons

How does it work: rangefinder by Cdang via wikimedia commons

It's all trigonometry lads, just triangles.
Sometimes they are bend over a sphere, that's a bit more mathy, but it's still triangles.

— A Chief Officer teaching a group of cadets.

---